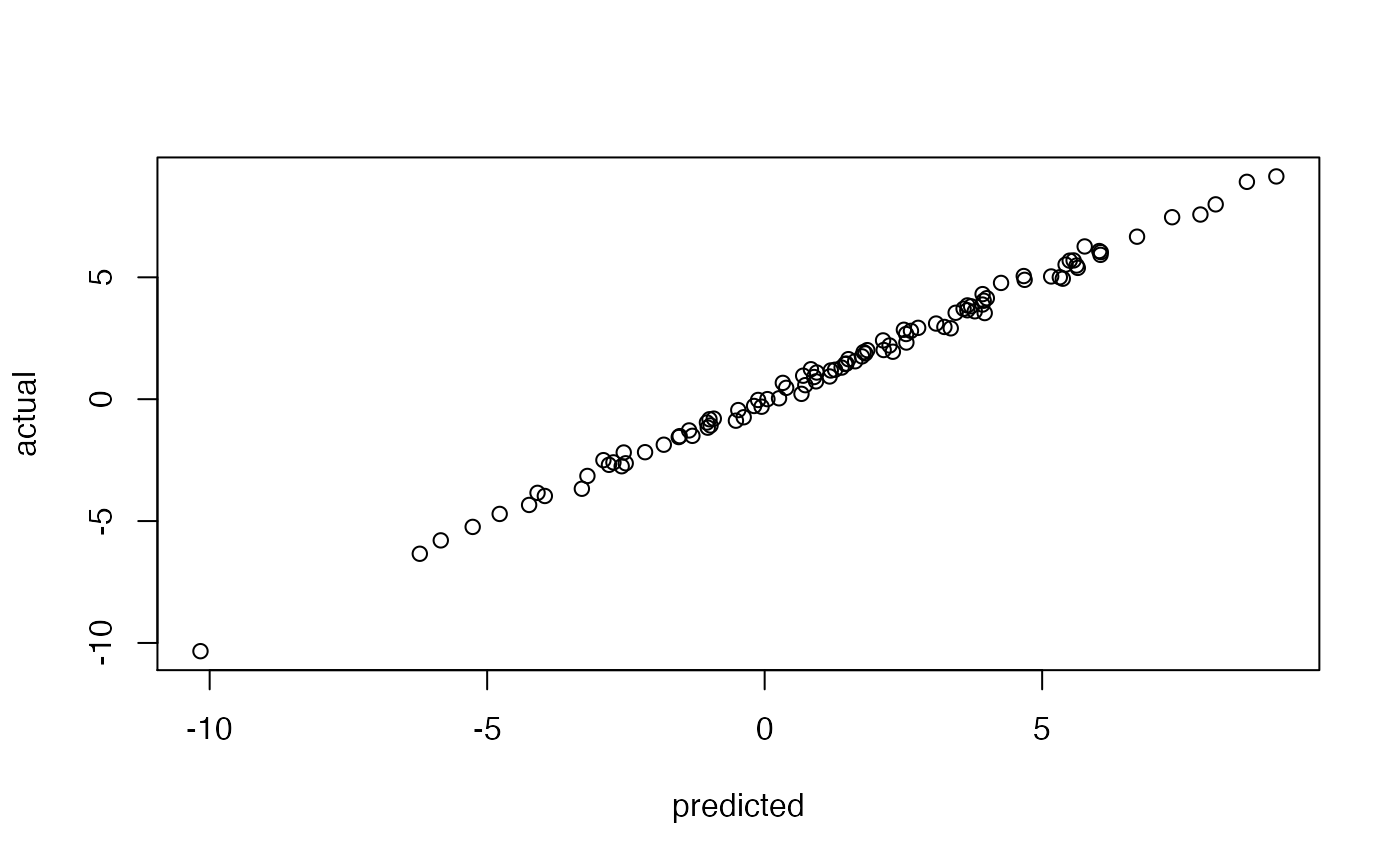
Model Predictions for HMC or MH

predict generates simulated data from the posterior predictive distribution. This simulated data can be used for posterior predictive check diagnostics from the bayesplot package

# S3 method for hmclearn
predict(object, X, fam = "linear", burnin = NULL, draws = NULL, ...)

Arguments

object	an object of class hmclearn, usually a result of a call to mh or hmc
X	design matrix, either from fitting the model or new data
fam	generalized linear model family. Currently "linear", "binomial", and "poisson" are supported
burnin	optional numeric parameter for the number of initial MCMC samples to omit from the summary
draws	Number of simulated values from the posterior conditioned on X
...	additional parameters, currently unsupported

Value

An object of class hmclearnpred.

Elements of hmclearnpred objects

y

Median simulated values for each observation in X

yrep

Matrix of simulated values where each row is a draw from the posterior predictive distribution

X

Numeric design matrix

References

Gabry, Jonah and Mahr, Tristan (2019). bayesplot: Plotting for Bayesian Models. https://mc-stan.org/bayesplot/

Gabry, J., Simpson, D., Vehtari, A., Betancourt, M., and Gelman, A (2019). Visualization in Bayesian Workflow. Journal of the Royal Statistical Society: Series A. Vol 182. Issue 2. p.389-402.

Examples

# Linear regression example
set.seed(521)
X <- cbind(1, matrix(rnorm(300), ncol=3))
betavals <- c(0.5, -1, 2, -3)
y <- X%*%betavals + rnorm(100, sd=.2)

f1 <- hmc(N = 500,
          theta.init = c(rep(0, 4), 1),
          epsilon = 0.01,
          L = 10,
          logPOSTERIOR = linear_posterior,
          glogPOSTERIOR = g_linear_posterior,
          varnames = c(paste0("beta", 0:3), "log_sigma_sq"),
          param=list(y=y, X=X), parallel=FALSE, chains=1)

summary(f1)
#> Summary of MCMC simulation
#> 
#>                    2.5%         5%        25%        50%        75%        95%
#> beta0         0.3761942  0.4648189  0.5155872  0.5325537  0.5497568  0.5781873
#> beta1        -1.0739748 -1.0488209 -1.0281105 -1.0118904 -0.9965476 -0.9627243
#> beta2         0.9617633  1.8882191  1.9997614  2.0164956  2.0314843  2.0521531
#> beta3        -3.0255286 -3.0154147 -2.9970442 -2.9807522 -2.9646554 -2.8305029
#> log_sigma_sq -3.2893269 -3.2522864 -3.1503169 -3.0392322 -2.9052983 -0.4878351
#>                   97.5%
#> beta0         0.5854330
#> beta1        -0.9602134
#> beta2         2.0591168
#> beta3        -1.8103326
#> log_sigma_sq  1.5343091

p <- predict(f1, X)
predvals <- p$y
plot(predvals, y, xlab="predicted", ylab="actual")

X2 <- cbind(1, matrix(rnorm(30), ncol=3))
p2 <- predict(f1, X2)
p2$y
#>  [1] -0.6990180  7.0555558  1.0823677 -3.9274742  2.1074708  1.1030894
#>  [7]  0.3838926  3.8462382 -2.4566947  2.3849477